투포인터 알고리즘이란?
1차원 배열에서 각자 다른 원소를 가리키고 있는
2개의 포인터를 이용해 문제를 해결하는 알고리즘이다.
대표적인 문제는 백준 1806 구간합 문제이다.
https://www.acmicpc.net/problem/1806
문제를 해설하며 알고리즘도 같이 설명하겠다.
문제해설
길이 n인 수열이 주어진다.
목표값이 주어지고
수열의 부분합 중에서 목표값 이상인
최소의 부분합 길이를 출력하면 된다.
문제풀이
투포인터 알고리즘의 핵심은 아래 코드이다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
while (right >= left) {
int nr = right, nl = left;
if (sum < t) {
if (right < n) {
right++;
sum += arr[right];
}
}
else {
if (left <= right) {
sum -= arr[left];
left++;
}
}
if (sum >= t)
res = min(res, right - left + 1);
if (nr == right && nl == left)
break;
}
코드만 봐서는 이해가 안되니 바로 아래 그림으로 설명하면
입력 수열은 5 1 3 5 10 7 4 9 2 8이고 목표값은 15이다.
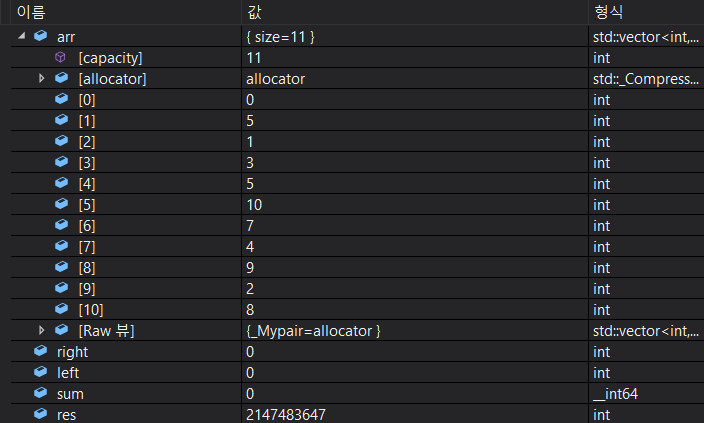
우선 right, left 둘다 초기값인 0을 가지고있다.
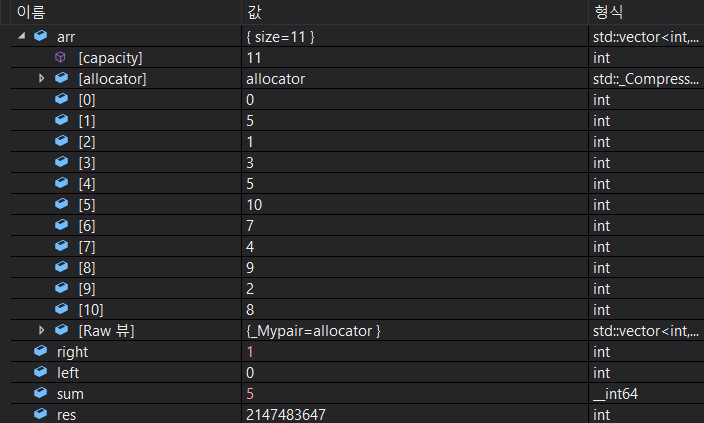
right가 한칸 이동하며 합도 0부터 1까지인 5로 바뀌었다.
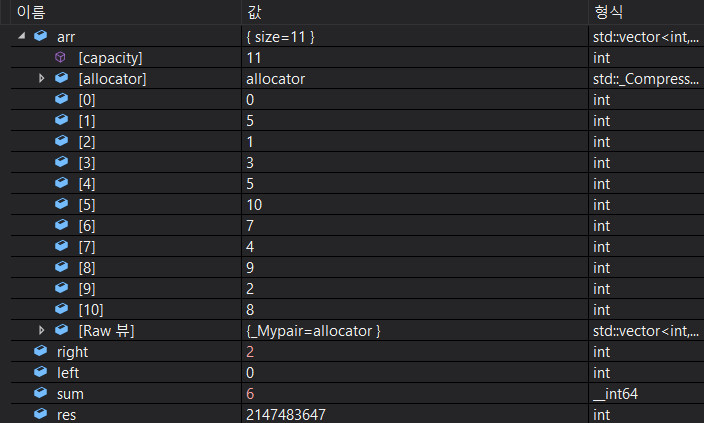
목표값이 도달하지 못했기 때문에 right가 한칸 더 움직인다.
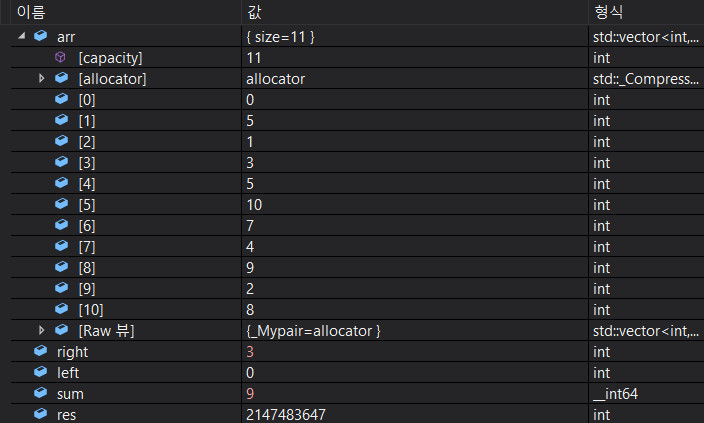
마찬가지로 한칸 더 움직인다.
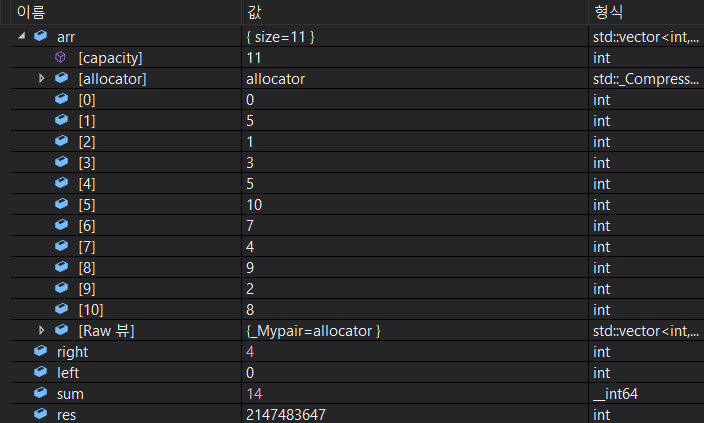
1이 부족하다 한칸더
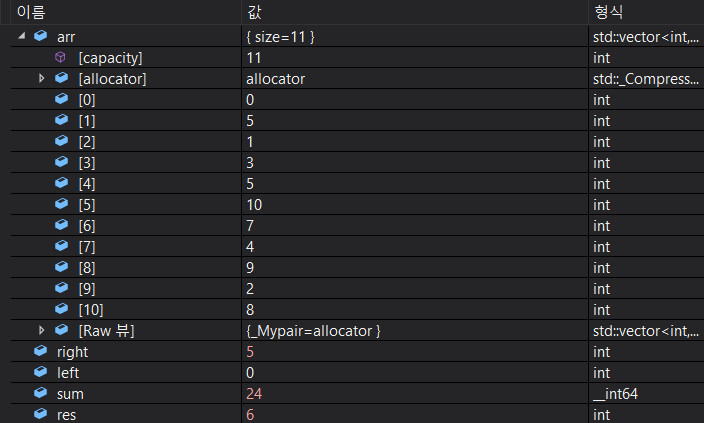
이제 0부터 5까지의 합이 24가 되었다.
목표치인 15를 넘었지만 우리는 최소길이의 수열을 찾아야 한다.
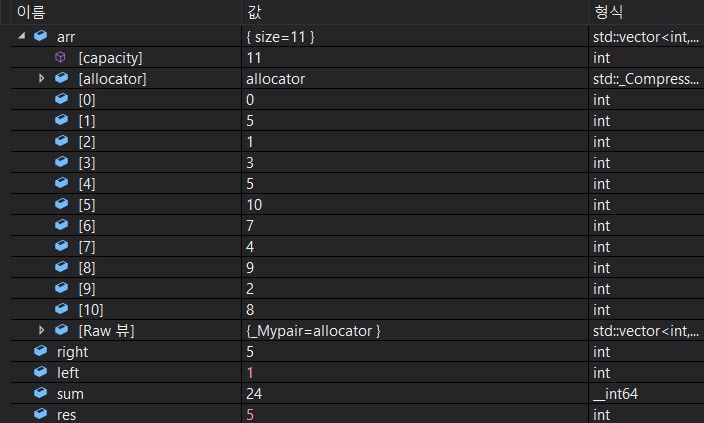
그러므로 이제 left가 한칸씩 움직인다.
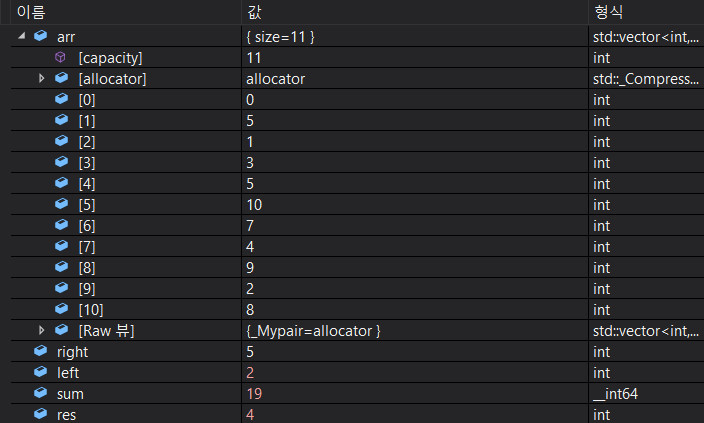
left가 2가 되면서 1의 값인 5가 합에서 빠졌다.
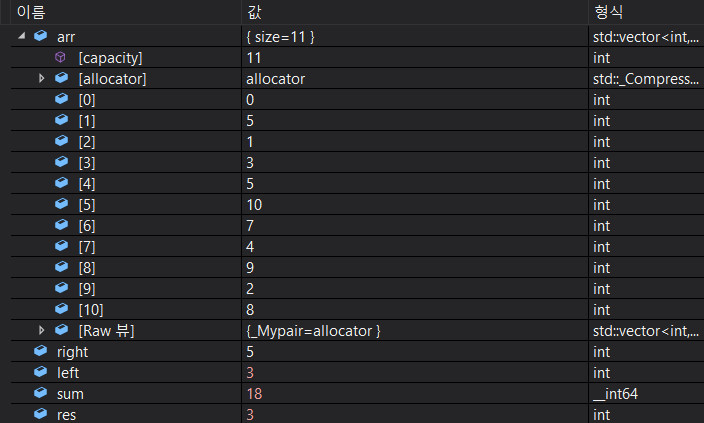
left가 한칸 더 움직여서 -1이 되었다.
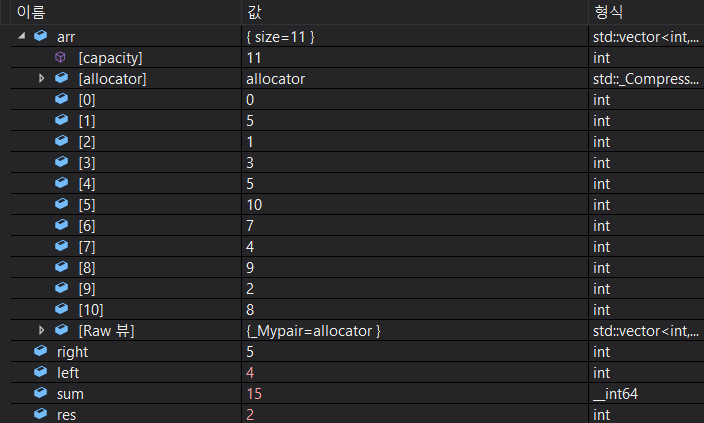
이제 left가 4까지 움직여서 4~5까지의 합이 15가 되었다.
다음 단계는 left가 한칸 더 움직여 합이 10이 되고
15보다 합이 작기 때문에 right가 움직이면서 다시 값이 커질 것이다.
이런식으로 배열 끝까지 탐색을 해주며 값을 갱신한다.
이 문제를 이중반복문으로 푼다면 시간복잡도가 O(N^2)이 되겠지만
투포인터 알고리즘을 쓴다면 탐색시간이 2N이므로 O(N)만에 문제가 풀린다.
전체코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include<iostream>
#include<algorithm>
#include<vector>
#include<limits.h>
using namespace std;
typedef long long ll;
int main() {
ios::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
int n, t; cin >> n >> t;
vector<int>arr(n + 1);
for (int i = 1; i <= n; i++)
cin >> arr[i];
ll sum = 0;
int right = 0, left = 0, res = INT_MAX;
while (right >= left) {
int nr = right, nl = left;
if (sum < t) {
if (right < n) {
right++;
sum += arr[right];
}
}
else {
if (left <= right) {
sum -= arr[left];
left++;
}
}
if (sum >= t)
res = min(res, right - left + 1);
if (nr == right && nl == left)
break;
}
if (res == INT_MAX)
cout << 0;
else
cout << res;
return 0;
}
